KuZ the Maximum spanning tree (Hard Version)
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
Time Limit: 2.0 s
Memory Limit: 1024.0 MB
Description
You are given N points, each in a multi-dimensional space with K coordinates. Imagine these points as locations that need to be connected with roads.
To connect these points, you will build roads where the cost of each road is determined by the Manhattan distance between the two points. For two points (\(A_{i1}\), \(A_{i2}\) ,,,, \(A_{iK}\)) and (\(A_{j1}\), \(A_{j2}\) ,,,, \(A_{jK}\)). Here, i, and j (1 <= i, j <= N && i != j) are the two points of the N and they will be connected by road, the cost to connect them is calculated as:
Cost(i , j) = ∣ \(A_{i1}\) - \(A_{j1}\) ∣ + ∣\(A_{i2}\) - \(A_{j2}\)∣ + ,,,, + ∣\(A_{iK}\) - \(A_{jK}\)∣.
Your goal is to connect all the points with a network of roads such that the total cost is maximized. This problem is about finding the Maximum Spanning Tree (MST) of the graph where:
- Each point is a vertex.
- Each road between points is an edge with weight equal to the Manhattan distance.
Note : The only difference between Easy version and Hard version is size of N
Input
The first line contains two integers: N (1 <= N <= \(2 * 10^5\)) (the number of points) and K(1 <= K <= 5) (the number of dimensions).
The next N lines each contain K integers, representing the coordinates of each point \(A_1\) , \(A_2\) ,,, \(A_K\) (1 ≤ \(A\) ≤ \(10 ^ {5}\)).
Output
Print a single integer which is the total cost of the Maximum Spanning Tree that connects all the points.
Sample
| Input | Output |
|---|---|
|
|
In this test case, After connecting each point,
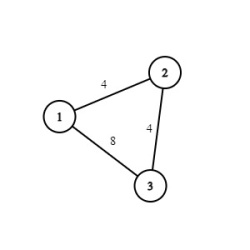
The maximum spanning tree will be of this graph
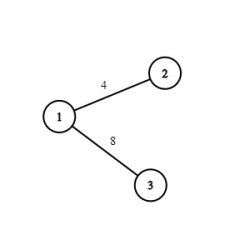
or
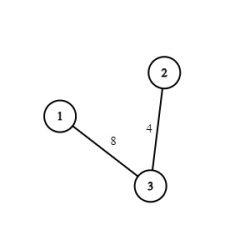
So the total cost of the Maximum Spanning Treee will be 12.
LU Divisonal Contest Problem Testing Round
- Status
- Done
- Rule
- ACM/ICPC
- Problem
- 11
- Start at
- 2024-11-30 19:30
- End at
- 2024-12-09 12:30
- Duration
- 209.0 hour(s)
- Host
- Partic.
- 15