You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

Time Limit: 2.0 s

Memory Limit: 256.0 MB

Description

You are given a tree with N nodes. Each node in the tree has an assigned value from the array A. The tree is rooted at node 1, and the tree is undirected and connected.

There are Q queries. For each query, you are asked to find the minimum number of changes required to make the values in the subtree rooted at a given node x a valid permutation. A valid permutation of size S is a sequence that contains all integers from 1 to S, exactly once.
For example,
[2,3,1], [4 ,3 ,2, 5, 1] are valid permutation, where [2,4,1], [1,1,2,3] are not.

The subtree rooted at a node x includes the node x itself and all its descendants.

Input

• The first line contains an interger T ( 1 ≤ T ≤ 5000), the number of test case.
  In each test case following line contains,
• The first line contains an integer N (1 ≤ N ≤ \(10^5\)) — the number of nodes in the tree.
• The second line contains an array A of length N, where A[i] (1 ≤ A[i] ≤ N) represents the value assigned to node i.
• The next N-1 lines describe the tree using N-1 edges. Each edge connects two nodes u and v (1 ≤ u,v ≤ N), meaning there is an edge between nodes u and v.
• The third line contains an integer Q (1 ≤ Q ≤ \(10^5\)) — the number of queries.
• The next line contains Q integer, x (1 ≤ x ≤ N) — the node for which the query is being made.

Sum of N overall test case dosen't exist \(10^5\).
Sum of Q overall test case doesn't exist \(10^5\).
Graph is a tree.

Output

For each query, output a single integer: the minimum number of changes needed to make the values in the subtree rooted at node x a valid permutation of the numbers 1, 2, ..., S, where S is the size of the subtree rooted at node x.

Sample

1
8
1 5 2 1 1 3 5 6
1 2
1 3
2 7
2 8
3 4
4 5
4 6
5
4 3 2 5 1

1
1
3
0
3

1st test case :

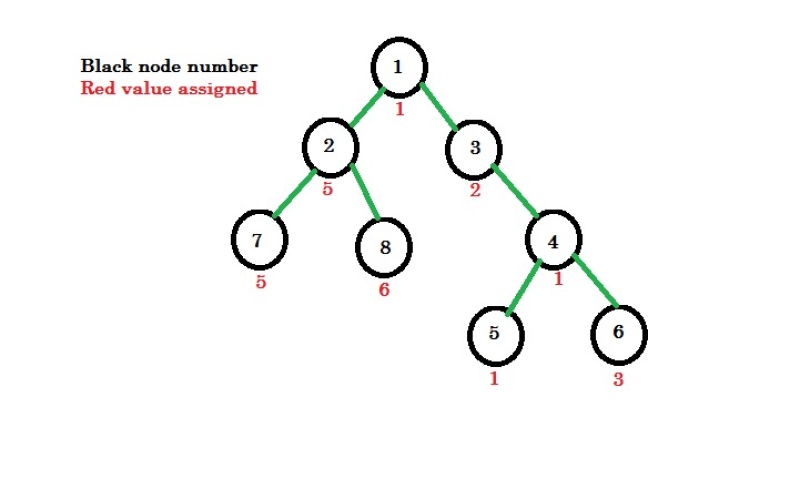
1st query : node x = 4,
node 4 has subtree, [4,5,6].
assingned value, [1,1,3].
total number of node this subtree is 3, we need to make permutation of length 3.
if we change 1st position value, [2,1,3], which is a 3 length permuation.
So only one change is requried, answer is 1.