Time Limit: 1.0 s

Memory Limit: 128.0 MB

Description

You are given a \(N * M\) grid. Currently you are \((x,y)\) position, you want to go \((p,q)\) position.
In each move you can go one of the following directions :

• if your current position (x,y), you can go (x-1 , y-1).
• if your current position (x,y), you can go (x+1 , y+1).
• if your current position (x,y), you can go (x-1 , y+1).
• if your current position (x,y), you can go (x+1 , y-1).

You can't move outside the grid but you can move any number of times in the grid. Your goal is to reach the destination.

Input

First line \(T\), number of test case.
In each test case, first line two positives integer \(N\) and \(M\).
Second line , \(x\) and \(y\).
Thrid line , \(p\) and \(q\).

\(1<=T<=10^5\)
\(1<=N,M<=10^9\)
\(1<=x,p<=N\)
\(1<=y,q<=M\)

Output

In each test case, if it's possible to reach destination print Yes, otherwise print No.

Sample

2
3 3
1 1
2 2
2 2
1 1
2 1

Yes
No

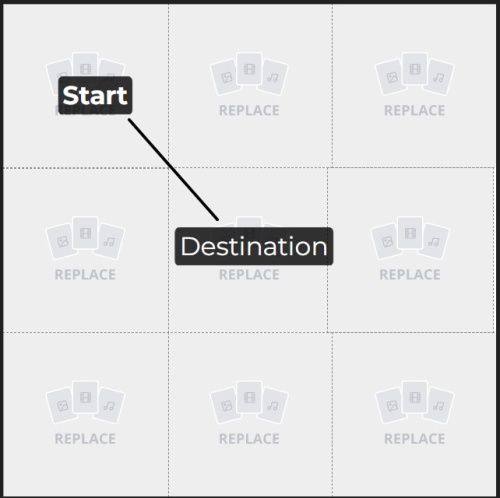
First test case :
\(3 * 3\) grid, current position (1,1) and destination position (2,2).
only one move required, we can increase x direction by 1 and y direction by 1. (1 + 1, 1 + 1) = (2, 2) = (p,q).