E1.Number of Ways (Easy version)
Time Limit: 1.0 s
Memory Limit: 128.0 MB
Description
You are given a binary array \(A[]\) and the length of the array is N. Binary array means this array element contains either 0 or 1.
You are also given a non-negative integer K.
- You need to remove some element (at least one or possibly all) from the array such way that, total sum of remaining element is greater than or equal to K.
Find the total number of ways you can remove some element from the array A[], after the remaining element total sum is greater than or equal to K.
The answer can be very large, so print it modulo by \(10^9+7\).
Note : An empty array A[] total sum is 0.
The only difference between the hard and easy versions is the limit of N.
Input
First line T, the number of test cases.
In each test case, first line N the length of array and a non-negative integer K.
Second line, an array \(A[]\) with exactly N elements.
\(1<=T<= 10^3\)
\(1<= N <= 5 * 10^3 \)
\(0<= K<= 10^6\)
\(A[] = 0 , 1 \)
Sum of N overall test case doesn't exceed \(5 * 10^3\)
Output
In each test case, print the total number of ways modulo by \(10^9 + 7 \)
Sample
| Input | Output |
|---|---|
|
|
First test case :
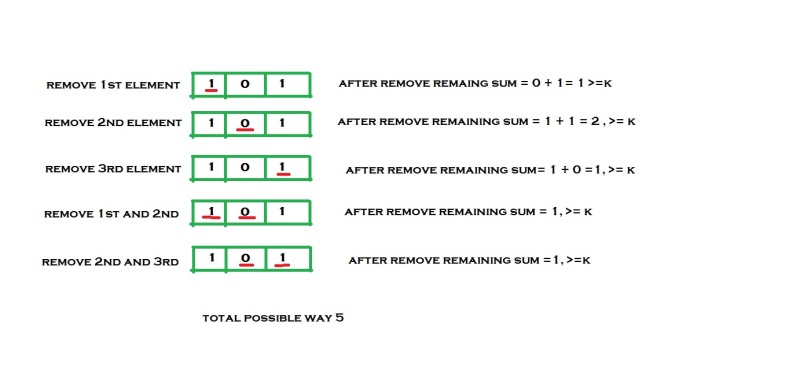
Information
- ID
- 1093
- Difficulty
- 5
- Category
- DP | Combinatorics Click to Show
- Tags
- # Submissions
- 103
- Accepted
- 26
- Accepted Ratio
- 25%
- Uploaded By
Related
In following contests: