F. Matrix Sum
Time Limit: 1.0 s
Memory Limit: 256.0 MB
Description
You are given a N x M matrix where N represent number of rows and M represent number of coloums. You need to rearrange this matrix such way that, two consecutive cell (it could be row or coloum) sum is maximize overall.
if N = 2 and M = 2, then N * M matrix should be like this:
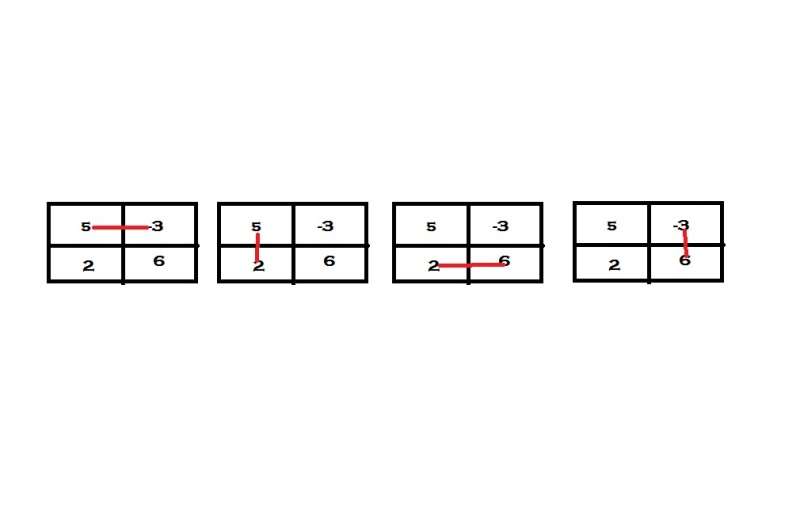
All possible consecutive cell sum marked in red colour.
(5,-3) = 5 + (-3) = 2
(5,2) = 5 + 2 = 7
(2,6) = 2 + 6 = 8
(-3,6) = -3 + 6 = 3.
So overall maximize sum is 2. (lowest sum in the matrix).
You need to rearrange matrix value such way that maximize sum is as maximum as possible.
Note : Two consecutive cell, not full coloum or row.
Input
First Line T, Number of test cases.
In each test case,
First line N and M, number of row and coloum, respectively.
Second line a matrix A[][] and the length of the matrix is \(N * M\).
\(1<=T<=10^3\)
\(1<=N,M<=500\) , \(N * M > 1\)
\(-10^3 <= A[][]<= 10^3\)
It is guranteed that sum of \(N * M\) over all test case does not exceed \(3 * 10^5\) .
Output
In each test case, print the maximize sum after rearrange the matrix.
Sample
| Input | Output |
|---|---|
|
|
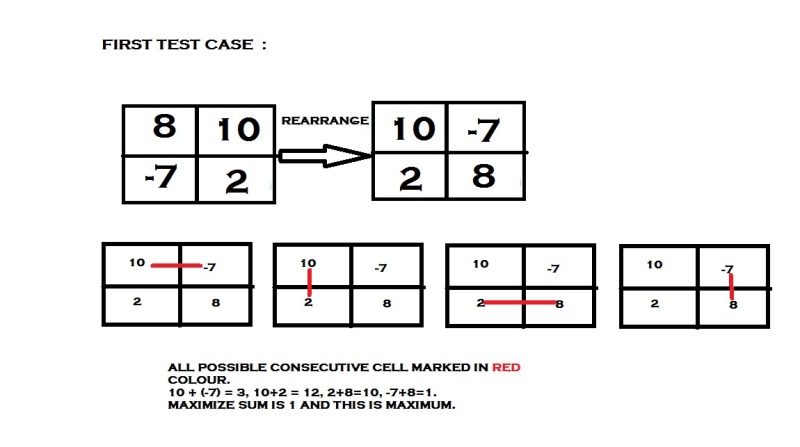
Information
- ID
- 1065
- Difficulty
- 6
- Category
- Implementation | Data_Structure Click to Show
- Tags
- # Submissions
- 31
- Accepted
- 5
- Accepted Ratio
- 16%
- Uploaded By
Related
In following contests: