E. Make Cycle in Tree
Time Limit: 1.0 s
Memory Limit: 256.0 MB
Description
You are given an undirected tree with \(N\) nodes (numbered \(1\) to \(N\)) and \(N–1\) edges.
• Node \(i\) has weight \(W_i\).
• Each existing edge \((U , V)\) has cost \(C_{U V}\).
You must add exactly one new edge between two nodes \(U\) and \(V\) that are not already directly connected. The cost of this new edge is defined to be the sum of the costs of all edges along the unique path from \(U\) to \(V\) in the original tree. Adding it creates exactly one simple cycle.
- Cycle weight = (sum of weights of all distinct nodes on the cycle) – (sum of costs of all edges on the cycle, including the new edge).
Find the maximum cycle weight over all choices of \(U\), \(V\).
Input
The first line contains an integer \(T\) (\(1 ≤ T ≤ 1000\)) — the number of test cases.
For each test case:
- The first line contains an integer \(N\) (\(3 ≤ N ≤ 2 * 10^5\)) — the number of nodes.
- The second line contains \(N\) integers (\(W_1, W_2, ... , W_N\)) (\(0 ≤ W_i ≤ 10^9\)) — the weights of the nodes.
- Then \(N-1\) lines follow, each containing three integers \(U, V, C\) (\(1 ≤ U,V ≤ N\)), (\(0 ≤ C≤ 10^9\))) — representing an edge between nodes \(U\) and \(V\) with cost \(C\).
The sum of N over all test cases does not exceed \(2 * 10^5\).
The given edges form a tree.
Output
For each test case, print one integer — the maximum cycle weight achievable by adding exactly one edge.
Sample
| Input | Output |
|---|---|
|
|
First test case :
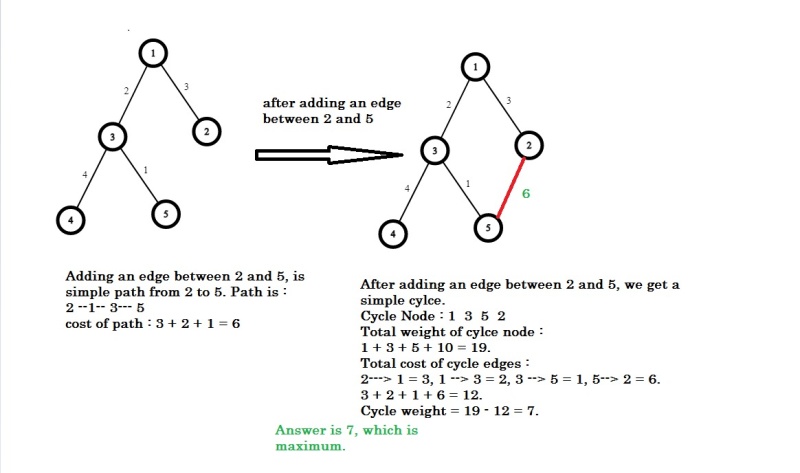
Information
- ID
- 1205
- Difficulty
- 8
- Category
- Graph_Theory | DP Click to Show
- Tags
- # Submissions
- 91
- Accepted
- 23
- Accepted Ratio
- 25%
- Uploaded By
Related
In following contests: